Hike News
Hike News

機器學習-Ridge回歸

Python機器學習 本文总阅读量次

Introduction

對線性模型進行訓練學習會變成複雜的模型
數據的特徵和目標值之間的關係，若不僅僅是線性關係，為了不斷地去擬合訓練集，會導致模型複雜度提高

underfitting & overfitting

過擬合與欠擬合

檢驗欠擬合或是過擬合：透過結果的現象判斷並通過交叉驗證得知訓練結果

  • 若再訓練過後結果不好，測試也不好：欠擬合
  • 若再訓練過後結果為非常好(99%-100%)，測試卻只有80-90%：過擬合

欠擬合(underfitting)

一個假設在訓練數據上不能獲得更好的擬合，但是在訓練數據外的數據集上也不能很好的擬合數據，此時認為這個假設出現了欠擬合現象(模型過於簡單)

  • 學習的特徵太少(訓練集與測試集皆表現不好)
  • 解決辦法：增加特徵的數量

過擬合(overfitting)

一個假設在訓練數據上能夠獲得比其他假設更好的擬合，但是在訓練數據外的數據集上卻不能很好的擬合數據，此時認為這個假設出現了過擬合現象(模型過於複雜)

  • 原始特徵過多，存在一些noise特徵，使其複雜化，因為模型會嘗試去兼顧各個測試數據點
  • 線性回歸(linearRegression)容易出現過擬合的情況，原因就是為了把訓練集的數據表現更好
  • 解決辦法
    • 進行特徵選擇，消除關聯性大的特徵(較難做)
    • 正則化 (在機器學習-特徵工程-降維 有提過)

正則化

在訓練過程中不同特徵的權重($w_1, w_2, …$)會持續更新
正則化便是不斷地調整，透過減少高次項特徵之權重$w$(趨近於0)，將回歸的結果不斷的smooth

  • 可使得$w$變小，使其與高次項特徵相乘時接近於0
  • 優點
    • 越小的參數說明模型越簡單
    • 越簡單的模型越不容易發生過擬合的現象

Ridge

使用Ridge回歸 解決過擬合的問題

  • 一種帶有L2正則化的線性回歸
  • 使用sklearn.linear_model.Ridge

Ridge(alpha=1.0)

  • 具有L2正則化的線性最小二乘法
  • alpha : 正則化力度($\lambda$, 超參數)
    • 通常介於0～1 or 1~10 之間
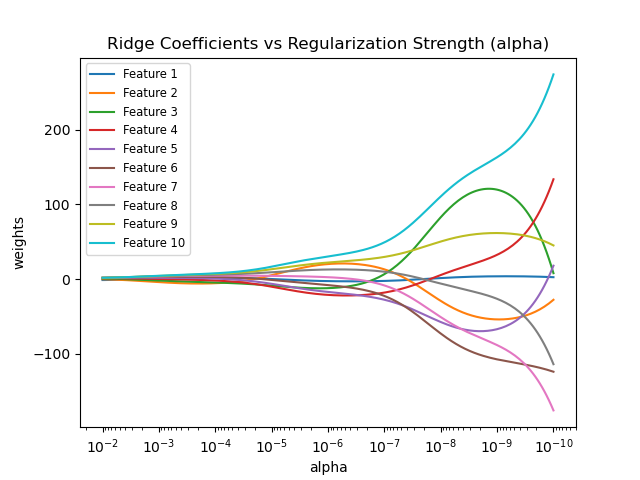
    • weights vs alpha
    • 力度越大的情況下，權重會趨向於0，model簡單化
  • 調用coef_屬性，查看最後回歸的權重

Example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

boston = load_boston()

def Ridge_test():
    X_train, X_test, y_train, y_test = train_test_split(boston.data,boston.target,test_size=0.25)

    StdS =  StandardScaler()
    X_train = StdS.fit_transform(X_train)
    X_test = StdS.transform(X_test)

    Rg = Ridge(alpha = 1.0)
    Rg.fit(X_train,y_train)
    print("權重\n",Rg.coef_)

    y_predict = Rg.predict(X_test)
    print("預測結果：\n",y_predict)

    print("均方誤差為：",mean_squared_error(y_test,y_predict))


if __name__ == '__main__':
    Ridge_test()

Result

1
2
3
4
5
6
7
8
9
10
11
權重
 [-0.82177747  1.20950534  0.06552334  0.60526014 -2.25725199  2.49725259
  0.00725436 -3.40161807  2.66837018 -2.28422927 -2.12014388  0.56002103
 -3.65238349]
預測結果：
 [16.96844917 20.71311538 15.5034732  23.45319042 21.04674699 24.9338077
 20.91414999 29.09249464 11.53948481 30.18469936 14.37130082 44.67833472
 ...
 ...
 22.40497723]
均方誤差為： 19.432609045304503

tips

  • 藉由Ridge得到的回歸係數更符合實際，且更可靠
  • 能讓估計參數的波動範圍變小，變得更穩定
  • 在存在異常數據偏多的研究中，有較大的實用價值
Python機器學習